Qızıl bölgü - Gözəlliyin riyazi formulu
Qızıl bölgü - Gözəlliyin riyazi formulu
Qızın bölgü (və ya qızıl nisbət) — riyaziyyat və incəsənətdə tətbiq olunur. İki ədəd o vaxt qızıl nisbətdə olur ki, onların cəminin daha böyüyünə nisbəti onlardan böyüyünün kiçiyinə nisbətinə bərabər olsun. Cəbri dildə aşağıdakı kimi yazılır:
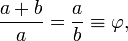
burada Yunan hərfi fi (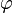
) qızıl bölgünü bildirir və onun dəyəri:
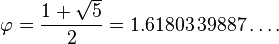
XX əsrdən başlayaraq xeyli sənətkarlar, memarlar öz işlərini qızıl bölgüyə əsasən qurmağa çalışıblar. Xüsusən də, onlar qızıl düzbucaqlı formasında tikintilərə xüsusi yer ayırıblar. Qızıl düzbucaqlıda uzun tərəfin qısa tərəfə nisbəti qızıl bölgü əsasında qurulur.
Qızıl Bölgü ilə dörtküncün yaranışı
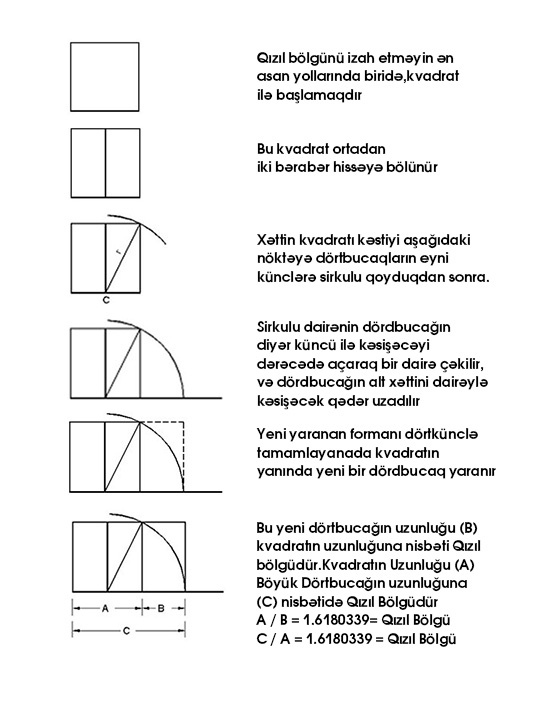
Bu dörtkünclərin hər birindən kvadrat çıxardıqda,yeni bir Qızıl Bölgülü dördbucaq yaranır.
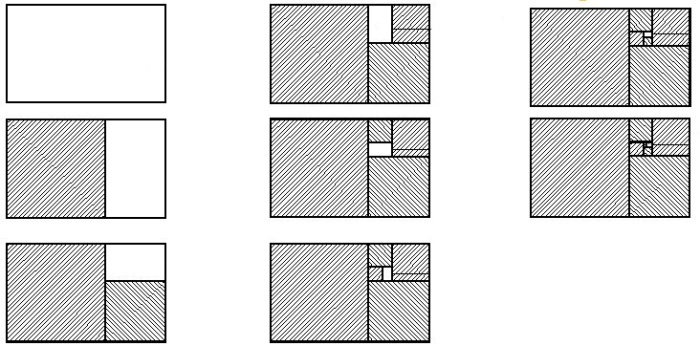
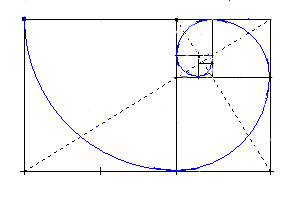
Qızıl bölgü ilə içindən dəfələrlə kvadratlar çıxartdığımız bu dördküncün kvadratlarının kənar uzunluqlarını alan bir çevrə hissəsini hər kvadratın içində çəksək, bir Qızıl Bölgülü Spiral yaranır. Bu Qızıl Bölgülü Spiral təbiətdə bir çox canlı və bitkilərdə görmək olur.
Qızıl bölgünün qısa tarixcəsi
Qızın bölgü tarixən insanlar tərəfindən istifadə edilməsinə baxmayaraq, ilk dəfə kim tərəfindən kəşf edildiyi haqqında dəqiq bir məlumat yoxdur. Euclid (e.ə. 365 – e.ə. 300), «Elementlər» adlı nəzəriyyəsində bir xətti 1.6180339… nöqtəsindən bölmək haqqında yazmış və bu xətti ekstrem və əhəmiyyətli nisbətdə bölmək deyə adlandırmışdı.
Misirlilər Xeops piramidasinin inşasında həm Pi həm də PHİ nisbətindən istifadə etmişdirlər.
Yunanlar Parthenonun bütün diyaznını Qızıl nisbətə uyğun şəkildə çəkmişdirlər.
Bu nisbəti məşhur Yunan heykəltartaş Parthenonun bütün əsərlərində istifadə etmişdir.
Leonardo Fibonacci adlı İtalyan riyaziyyatcı “Fibonacci rəqəmləri” adlı rəqəmlərin müəyyən sıralamasını kəşf etmişdir.
Leonardo Da Vinci 1509-cu ildə Luca Paciolunun dərc etdiyi “İlahi Nisbət” adlı rəsmləri verilmişdir. Bu kitabda Leonardo Da Vinci tərəfindən hazırlanmış Five Platonic Solids (beş platonik cism) adlı rəsmlər mövcuddur. Bunlar eyniylə bir kub, bir tetrahedron, bir dodekahedron, bir oktahedron və bir ikosahedronun rəsmləridir.
Qızıl bisbətin latın dilində ilk istifadə edən böyük ehtimalla Leonardo Da Vinçidir. Renensans dövrünün rəssamları rəsmlərində və heykəllərində tarazılıq və gözəlliyi əldə etmək üçün Qızıl Bölgünü çox vaxt istifadə etmişdirlər.
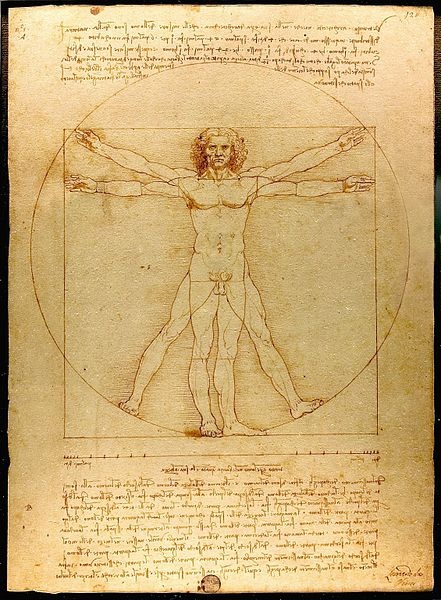
Leonardo Da Vincinin gündəliyinin içərisində olan, insan və təbiəti bir-biri ilə əlaqələndirən və bütünləşdirən əsəri üçün bir dönüş nöqtəsi olaraq qəbul edilən və insan bədənindəki nisbətləri göstərən Vitruvius Adam əsəri (1492)
Leonardo Da vinci, Last Supper (Son şam yeməyi) adlı tablosunda, İsanın və müridlərin oturduğu stolun ölçüsündən,arxadakı divar və pəncərələrə qədər Qızıl Bölgünü tətbiq etmişdir.
Jahanes Kepler(1571-1630) Qızılk bölgünü belə ifadə etmişdir :”Qeometriyanın iki böyük xəzinəsi vardır; biri Pifaqor teoriyası, o biri bir xəttin Qızıl bölgüyə görə bölünməsidir”. Bu nisbəti görsətmək üçün Parthenon’un memarı və bu bölgünü ilk istifadə edən Phidiasa həsr edərək 1900-cü illərdə Yunan əlifbasındaki Phi hərfini Amerikalı riyaziyyatcı Mark Barr istifadə etmişdir. Eyni zamanda Yunan əlifbasındaki qarşılığı F hərfi də Fibonaccinin ilk hərfidir.
Fibonacci Rəqəmləri və Qızıl Bölgü
Fibonacci rəqəmləri Fibonaççinin Liber Abaçi kitabında dovşanların artımı ilə bağlı araşdırmaları nəticəsində Fibonaççi tərəfindən ortaya qoyulmuşdu. Tarixə əsasən, ilk iki Fibonaççi ədədləri 0 və 1-dir. Sonra gələn ədəd özündən əvvəlki ilk iki qonşusunun cəminə bərabərdir. Bəzi mənbələrdə sıranın ilk ədədi 0 yox, 1 götürülür. Riyazi dildə, Fibanoççi sırası Fn aşağıdakı rekkurent düsturla verilir harda ki, F0 = 0 və F1 = 1.
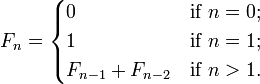
Fibonaççi sırası Pizali Leonardonun adı ilə bağlıdır. Fibanoççi ədədləri arasında nisbət 1,618-dir. O, qədim misirlilər tərəfindən tapılmış və Pifaqor ondan riyaziyyatda istifadə etmişdir. Bu, tamın iki qeyri-bərabər, lakin proporsional hissələrə bölmənin nəticəsidir. Vaxtı ilə bunu «ilahə proporsiya», «qızıl bölgü» adlandırmışlar, sonra isə Leonardo da Vinçi proporsiyanı ifadə etmək üçün ümumi qəbul edilmiş termin – «qızıl kəsik»dən istifadə etmişdir. O vaxtdan bu proporsiya bir çox təbii hadisələrdə tapılmışdır: bədənimizin quruluşunda, botanikada, kvant mexanikası proseslərində və s.
Hazırda qızıl kəsik praktiki fəaliyyətdə istifadə olunur — riyaziyyatda, texnikada, musiqidə, estetikada və s. İnsanın inkişafı da həmçinin bu proporsiyaya müvafiq baş verir. Həyatımızın yaradıcılıq mexanizminin bu və ya digər dominantaları ilə mərhələlərə bölərək onun ədədlərinin qanununa tabe olur.
Qızıl Bölgü bir rəqəmin insanlıq, elm və incəsənət tarixində oynadığı möhtəşəm bir roldur. Phi (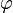
) bəşriyyəti və həyatı dərk etmək mövzusunda bizə yeni qapılar açmağa kömək edəcəkdir.
israfilmuradli.wordpress.com
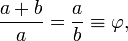
burada Yunan hərfi fi (
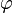) qızıl bölgünü bildirir və onun dəyəri: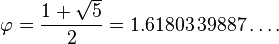 XX əsrdən başlayaraq xeyli sənətkarlar, memarlar öz işlərini qızıl bölgüyə əsasən qurmağa çalışıblar. Xüsusən də, onlar qızıl düzbucaqlı formasında tikintilərə xüsusi yer ayırıblar. Qızıl düzbucaqlıda uzun tərəfin qısa tərəfə nisbəti qızıl bölgü əsasında qurulur.
Qızıl Bölgü ilə dörtküncün yaranışı
Bu dörtkünclərin hər birindən kvadrat çıxardıqda,yeni bir Qızıl Bölgülü dördbucaq yaranır.
Qızıl bölgü ilə içindən dəfələrlə kvadratlar çıxartdığımız bu dördküncün kvadratlarının kənar uzunluqlarını alan bir çevrə hissəsini hər kvadratın içində çəksək, bir Qızıl Bölgülü Spiral yaranır. Bu Qızıl Bölgülü Spiral təbiətdə bir çox canlı və bitkilərdə görmək olur.
Qızıl bölgünün qısa tarixcəsi
Qızın bölgü tarixən insanlar tərəfindən istifadə edilməsinə baxmayaraq, ilk dəfə kim tərəfindən kəşf edildiyi haqqında dəqiq bir məlumat yoxdur. Euclid (e.ə. 365 – e.ə. 300), «Elementlər» adlı nəzəriyyəsində bir xətti 1.6180339… nöqtəsindən bölmək haqqında yazmış və bu xətti ekstrem və əhəmiyyətli nisbətdə bölmək deyə adlandırmışdı.
Misirlilər Xeops piramidasinin inşasında həm Pi həm də PHİ nisbətindən istifadə etmişdirlər.
Yunanlar Parthenonun bütün diyaznını Qızıl nisbətə uyğun şəkildə çəkmişdirlər.
Bu nisbəti məşhur Yunan heykəltartaş Parthenonun bütün əsərlərində istifadə etmişdir.
Leonardo Fibonacci adlı İtalyan riyaziyyatcı “Fibonacci rəqəmləri” adlı rəqəmlərin müəyyən sıralamasını kəşf etmişdir.
Leonardo Da Vinci 1509-cu ildə Luca Paciolunun dərc etdiyi “İlahi Nisbət” adlı rəsmləri verilmişdir. Bu kitabda Leonardo Da Vinci tərəfindən hazırlanmış Five Platonic Solids (beş platonik cism) adlı rəsmlər mövcuddur. Bunlar eyniylə bir kub, bir tetrahedron, bir dodekahedron, bir oktahedron və bir ikosahedronun rəsmləridir.
Qızıl bisbətin latın dilində ilk istifadə edən böyük ehtimalla Leonardo Da Vinçidir. Renensans dövrünün rəssamları rəsmlərində və heykəllərində tarazılıq və gözəlliyi əldə etmək üçün Qızıl Bölgünü çox vaxt istifadə etmişdirlər.
Leonardo Da Vincinin gündəliyinin içərisində olan, insan və təbiəti bir-biri ilə əlaqələndirən və bütünləşdirən əsəri üçün bir dönüş nöqtəsi olaraq qəbul edilən və insan bədənindəki nisbətləri göstərən Vitruvius Adam əsəri (1492)
Leonardo Da vinci, Last Supper (Son şam yeməyi) adlı tablosunda, İsanın və müridlərin oturduğu stolun ölçüsündən,arxadakı divar və pəncərələrə qədər Qızıl Bölgünü tətbiq etmişdir.
Jahanes Kepler(1571-1630) Qızılk bölgünü belə ifadə etmişdir :”Qeometriyanın iki böyük xəzinəsi vardır; biri Pifaqor teoriyası, o biri bir xəttin Qızıl bölgüyə görə bölünməsidir”. Bu nisbəti görsətmək üçün Parthenon’un memarı və bu bölgünü ilk istifadə edən Phidiasa həsr edərək 1900-cü illərdə Yunan əlifbasındaki Phi hərfini Amerikalı riyaziyyatcı Mark Barr istifadə etmişdir. Eyni zamanda Yunan əlifbasındaki qarşılığı F hərfi də Fibonaccinin ilk hərfidir.
Fibonacci Rəqəmləri və Qızıl Bölgü
Fibonacci rəqəmləri Fibonaççinin Liber Abaçi kitabında dovşanların artımı ilə bağlı araşdırmaları nəticəsində Fibonaççi tərəfindən ortaya qoyulmuşdu. Tarixə əsasən, ilk iki Fibonaççi ədədləri 0 və 1-dir. Sonra gələn ədəd özündən əvvəlki ilk iki qonşusunun cəminə bərabərdir. Bəzi mənbələrdə sıranın ilk ədədi 0 yox, 1 götürülür. Riyazi dildə, Fibanoççi sırası Fn aşağıdakı rekkurent düsturla verilir harda ki, F0 = 0 və F1 = 1.
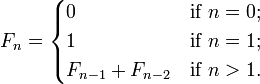
Fibonaççi sırası Pizali Leonardonun adı ilə bağlıdır. Fibanoççi ədədləri arasında nisbət 1,618-dir. O, qədim misirlilər tərəfindən tapılmış və Pifaqor ondan riyaziyyatda istifadə etmişdir. Bu, tamın iki qeyri-bərabər, lakin proporsional hissələrə bölmənin nəticəsidir. Vaxtı ilə bunu «ilahə proporsiya», «qızıl bölgü» adlandırmışlar, sonra isə Leonardo da Vinçi proporsiyanı ifadə etmək üçün ümumi qəbul edilmiş termin – «qızıl kəsik»dən istifadə etmişdir. O vaxtdan bu proporsiya bir çox təbii hadisələrdə tapılmışdır: bədənimizin quruluşunda, botanikada, kvant mexanikası proseslərində və s.
Hazırda qızıl kəsik praktiki fəaliyyətdə istifadə olunur — riyaziyyatda, texnikada, musiqidə, estetikada və s. İnsanın inkişafı da həmçinin bu proporsiyaya müvafiq baş verir. Həyatımızın yaradıcılıq mexanizminin bu və ya digər dominantaları ilə mərhələlərə bölərək onun ədədlərinin qanununa tabe olur.
Qızıl Bölgü bir rəqəmin insanlıq, elm və incəsənət tarixində oynadığı möhtəşəm bir roldur. Phi (
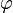) bəşriyyəti və həyatı dərk etmək mövzusunda bizə yeni qapılar açmağa kömək edəcəkdir. israfilmuradli.wordpress.com
