Fibonaççi silsiləsi
Fibonaççi silsiləsi
(0), 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584….

Fibonaççi İtaliyada 1170-ci ildə dünyaya gəlmiş orta əsr Avropasının ən böyük riyaziyyatçılarından olub. Əsl adı Leonardo Pizalı (Leonardo Pisanus) olan Fibonaççi əsasən “Fibonaççi ardıcıllığı” ilə tanınınır.
Leonardonun atası tacir olduğu üçün tez-tez oğlu ilə birgə Əlcəzairə səyahətlər edirdi elə orada o ərəb müəllimlərindən təhsil alırdı. Bundan sonra Fibonaççi Misirə ,Suriyaya ,Bizansa ,Sicilyaya səyahətlər etdi. O ,ərəb dilində qədim antik və hind riyaziyyatçılarının yazıları ilə tanış oldu. Bundan sonra o ilk kitabını – “Liber Abaci” yazır. Burada o romalıların çətin hesablamasının əvəzində hind rəqəmlərinin səmərəli istifadəsi və hesablanması haqda bilgilər vermişdir.
Leonardo heç vaxt özünü Fibonaççi adlandırmamışdır. Ona bu ləqəbi “Guglielmo Libri” 1838-ci ildə vermişdir. Fibonaççi sözü iki sözün qısaltmasıdır. “filius Bonacci” hansı ki, “Liber Abaci” kitabının üz qabığında olan sözlərdir. Bu ya “Bonaççonun oğlu” ya da Bonaççini soyad olaraq qəbul etsək “Bonaççoların oğlu”. Digər versiyaya görə Bonaçço sözünü uğurlu mənasında da tərcümə edə bilərik. Leonardonun “Liber abaci (1202-1228)”, “Practica geometriae (1220)”, “Flos (1225)”, “Liber quadratorum (1225)” və s. Kitabları var.
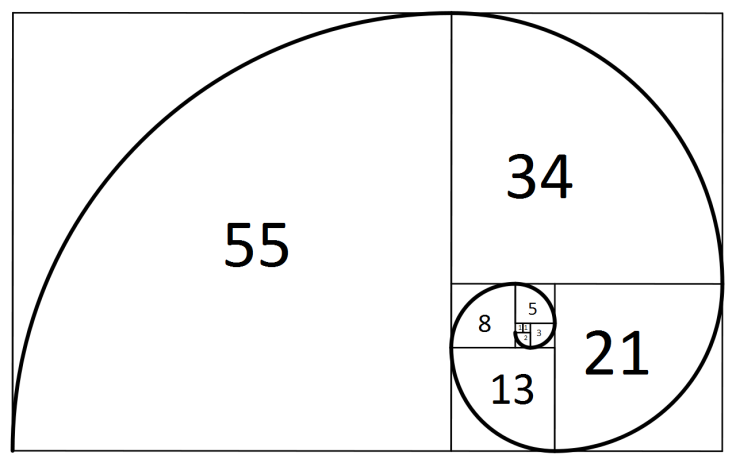
Əgər yuxarıdakı ardıcıllıqı tanımırsızsa azca baxıb məntiqi işlədib silsilədəki ardıcıllığın düsturunu tapmağınız yaxşı olar. Hər sonrakı ədəd özünkündən əvvəlki ədədlərin cəmi şəklində davam edən bu ardıcıllığa Fibonaççi ardıcıllığı deyilir. F0=0, F1=1, Fn=Fn-1+Fn-2, n ≥2. Daha rahat dildə desək hər ədəd özündən əvvəl gələn iki ədədin cəminə bərabərdi. Burdan biz Fn=Fn+2-Fn+1 alarıq. Bu halda da Fibonaççi ədələrinin təkcə natural ədədlərə aid olmadığını görə bilərik. F-n=(-1)n+1Fn .


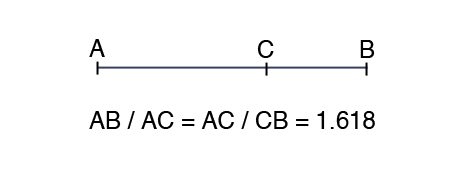
Əgər hər bir ədədi özündən əvvəlki ədədə bölsək qismət getdikcə 1.618 ədədinə yaxınlaşacaq. Bu da “Golden ratio” kimi tanınır.
Fibonaççi ədədlərini əsrlərdir bu qədər əhəmiyyətli edən səbəblər…
Fibonaççi ardıcıllığı təbiətdə tez-tez qarşımıza çıxar. Bu ədədlər istifadə edilərək alınan kəsrlər bizə «Qızıl bölgü» verir. «Qızıl bölgü»nü qədim misirlilər və yunanlılar tapmış və daha çox memarlıqda istifadə etmişdilər. Sadə mənası ilə «Qızıl bölgü» bütünün parçaları arasında olan həndəsi və ədədi bir nisbət əlaqəsidir.

Fibonaççi İtaliyada 1170-ci ildə dünyaya gəlmiş orta əsr Avropasının ən böyük riyaziyyatçılarından olub. Əsl adı Leonardo Pizalı (Leonardo Pisanus) olan Fibonaççi əsasən “Fibonaççi ardıcıllığı” ilə tanınınır.
Leonardonun atası tacir olduğu üçün tez-tez oğlu ilə birgə Əlcəzairə səyahətlər edirdi elə orada o ərəb müəllimlərindən təhsil alırdı. Bundan sonra Fibonaççi Misirə ,Suriyaya ,Bizansa ,Sicilyaya səyahətlər etdi. O ,ərəb dilində qədim antik və hind riyaziyyatçılarının yazıları ilə tanış oldu. Bundan sonra o ilk kitabını – “Liber Abaci” yazır. Burada o romalıların çətin hesablamasının əvəzində hind rəqəmlərinin səmərəli istifadəsi və hesablanması haqda bilgilər vermişdir.
Leonardo heç vaxt özünü Fibonaççi adlandırmamışdır. Ona bu ləqəbi “Guglielmo Libri” 1838-ci ildə vermişdir. Fibonaççi sözü iki sözün qısaltmasıdır. “filius Bonacci” hansı ki, “Liber Abaci” kitabının üz qabığında olan sözlərdir. Bu ya “Bonaççonun oğlu” ya da Bonaççini soyad olaraq qəbul etsək “Bonaççoların oğlu”. Digər versiyaya görə Bonaçço sözünü uğurlu mənasında da tərcümə edə bilərik. Leonardonun “Liber abaci (1202-1228)”, “Practica geometriae (1220)”, “Flos (1225)”, “Liber quadratorum (1225)” və s. Kitabları var.

Əgər yuxarıdakı ardıcıllıqı tanımırsızsa azca baxıb məntiqi işlədib silsilədəki ardıcıllığın düsturunu tapmağınız yaxşı olar. Hər sonrakı ədəd özünkündən əvvəlki ədədlərin cəmi şəklində davam edən bu ardıcıllığa Fibonaççi ardıcıllığı deyilir. F0=0, F1=1, Fn=Fn-1+Fn-2, n ≥2. Daha rahat dildə desək hər ədəd özündən əvvəl gələn iki ədədin cəminə bərabərdi. Burdan biz Fn=Fn+2-Fn+1 alarıq. Bu halda da Fibonaççi ədələrinin təkcə natural ədədlərə aid olmadığını görə bilərik. F-n=(-1)n+1Fn .


Əgər hər bir ədədi özündən əvvəlki ədədə bölsək qismət getdikcə 1.618 ədədinə yaxınlaşacaq. Bu da “Golden ratio” kimi tanınır.

Fibonaççi ədədlərini əsrlərdir bu qədər əhəmiyyətli edən səbəblər…
Fibonaççi ardıcıllığı təbiətdə tez-tez qarşımıza çıxar. Bu ədədlər istifadə edilərək alınan kəsrlər bizə «Qızıl bölgü» verir. «Qızıl bölgü»nü qədim misirlilər və yunanlılar tapmış və daha çox memarlıqda istifadə etmişdilər. Sadə mənası ilə «Qızıl bölgü» bütünün parçaları arasında olan həndəsi və ədədi bir nisbət əlaqəsidir.
- İnsan üzü- Qulaqlar arasındakı məsafə, gözlə üst dodaq arasında, burnun altı ilə çənə arasındakı məsafə qızıl nisbətdir.
- İnsanın işarə barmağı-Bir insanın işarə barmağı (normal standartlardakı barmaqlar üçün etibarlı) hər bir hissəsi bir əvvəlki hissəyə nisbəti Fibonaççi sayını verir. Qolumuzun üst hissəsinin alt hissəyə nisbəti qızıl nisbətdir.
- Misir piramidaları- Hər bir piramidanın döşəməsinin yüksəkliyinə nisbəti qızıl nisbəti verir.
- Bitkilər- Bitkinin sapındaki yarpaqların, bir ağacın budaqlarının nizamında hər zaman qızıl nisbət qaydası vardır. Yarpaqlardan biri başlanğıc nöqtəsi olaraq alındığında, bundan başlayaraq yuxarıya doğru (aşağıya doğru da ola bilər) sayılarsa, Fibonaççi ədədlərini verər.
