Planimetriya və stereometriya aksiomları
Planimetriya və stereometriya aksiomları
Həndəsə kursunun məntiqi qurulmasında aksiomların müstəsna əhəmiyyatini nəzərə alaraq planimetreyanın aksiomlarını yadımıza salaq:
Həndəsənin fəza fiqurlarını öyrənən bölməsi stereometriya (yunan sozü: Stereos- fəza, metreo-ölçürəm) adlanır. Streometriyada baxılan bütün nöqtələr çoxluğuna fəza deyilir.
Stereometriyada üç anlayış: nöqtə, düz xətt və müstəvi tərifsiz qəbul olunur.Həndəsədə istənilən nöqtələr çoxluğu fiqur adlanır. Nöqtə, düz xətt, müstəvi və fəza da fiqurlardır.

Planimetriyada bilidiyimiz bütün işarələr stereometriyada da öz mənasında işlədilir. Müstəviləri, adətən, yunan əlifbasının kiçik hərfləri ilə işarə edirlər. α, β, γvə s. A, B və C nöqtələrindən keçən müstəvini isə (α, β) kimi işarə edirlər.
Əsas anlayişlarin ən mühüm xassələri streometriya aksiomlarında ifadə olunur.
AKSİOM 1 ( aidlik aksiomu)
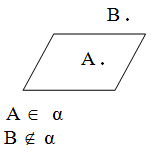
Fəzada düz xəttlər və müstəvilər var. Hər bir düz xəttə və hər bir müstəviyə aid olan və aid olmayan nöqtələr var.
AKSİOM 2 ( Müstəvi aksiomu)
Bir düz xətt üzərində olmayan üç nöqtədən bir və yalnız bir müstəvi keçir
AKSİOM 3 ( planametriya aksiomu)
Planametriyanıın bütün alsiomları və teoremləri fəzanın hər bir müstəvisində doğrudur.

Fəzada müstəvilərin iki qarşılıqlı vəziyyəti ola bilər, ortaq nöqtəsi olan müstəvilərə kəsişən, ortaq nöqtəsi olmayan müstəvilərə kəsişməyən müstəvilər deyilir.
AKSİOM 4 ( Müstəvilərin kəsişmə aksiomu)
İki müxtəlif müstəvinin ortaq nöqtəsi varsa, onlar bu nöqtələrdən keçən düz xətt boyunca kəsişirlər
AKSİOM 5 ( Fəzanın bölünməsi aksiomu)
Fəzadakı hər bir müstəvi fəzanın bu müstəviyə aid olmayan nöqtələrini aşağıdakı şərti ödəyən iki çoxluğa ayrılır:

α müstəvisi ilə bu çoxluqların birindən ibarət fiqura sərhəddi α müstəvisi olan yarımfəza deyilir.
Müxtəlif müstəvilərdə yerləşən qabarıq çoxbucaqların bərabərliyi və oxşarliğı da planimetriyada olduğu kimi qəbul edilir.
- Aidolma aksiomu. Düz xəttin üzərində olan nöqtələr və onun üzərində olmayan nöqtələr var.
- Düz xətt aksiomu. İki nöqtədən bir yalnız bir düz xətt keçir.
- Nöqtələrin düz xətt üzərində yerləşməsi aksionu. Düz xəttin ixtiyari 3 nöqtəsindən biri yalniz biri qalan ikisi arasında yerləşir.
- Düz xəttin bölünməsi aksionu. Düz xəttin ixtiyari A nöqtəsi bu düz xəttin qalan nöqtələrini aşağıdakı şərtləri ödəyən iki çoxluğa ayırır: eyni çoxluğa aid iki nöqtə A nöqtəsinin bir tərəfində yerləşir, müxtəlif çoxluqlara aid iki nöqtə A nöqtəsinin müxtəlif tərəfində yerləşir.
- Parçaların ölçülməsi aksiomu. Uzunluq vahidi seçməklə hər bir parçanın uzunluğunu ölçmək olar, yəni onun uzunluğunu müsbət ədədlə ifadə etmək olar.
- Parçaların toplanması aksiomu. Parçanın uzunluğu, onun hər hansı daxili nöqtəsi ilə bölündüyü parçanın uzunluqları cəminə bərabərdir.
- Parçanın ayrılması aksiomu. Şüanın baılanğıcından uzunluğu verimiş, bir və yalnız bir parça ayırmaq olar.
- Bucaqın ölçülməsi aksiomu. Hər bir bucağın sıfırdan böyük müəyyən dərəcə ölçüsü var. Açıq bucaq 1800 – yə bərabərdir.
- Bucaqların toplanması alsiomu. Bucağın dərəcə ölçüsü, onun daxili şüası ilə bölündüyü bucaqların dərərcə ölçüləri cəminə bərabərdir
- Tusi – Paş aksiomu. Üçbacağın təpələrindən keçməyən düz xətt onun bir tərəfini kəsirsə, onda həmin düz xətt digər iki tərəfdən yalnız birini kəsir.
- Bucağın ayrılması aksiomu. Istənilən şüadan başlayaraq verilmiş yarım müstəvidə bir tərəfi həmin süa olan və dərəcə ölçüsü 1800-dən kiçik bir yalnız bir bucaq qurmaq olar.
- Üçbucaqların bərabərliyini birinci əlaməti. Bir üçbacağın iki tərəfi və onlar arasındakı bucaq, uyğun olraq, o biri üçbucaqın iki tərərfi və onlar arasındakı bucağa bərabərdirsə, bu üçbucaqlar bərabərdir.
- Paralellik aksiomu. Düz xətttin üzərində olmayan nöqtədən bu düz xətt ən çoxu bir paralel düz xətt çəkmək olar.
- Sahənin varlığı aksiomu Hər bir sadə fiqurun seçilmiş ölçü vahidi ilə ifadə olunan müsbət sahəsi var
- Sahənin bərabərlik aksiomu. Bərabər üçbucaqların sahələri bərabərdir.
- Sahənin toplanması aksiomu. Əgər sadə fiqur ortaq daxili nöqtəsi olmayan sonlu sayda sadə fiqurlardan ibarətdirsə, bu fiqurun sahəsi onun hissələrinin sahəsi cəminə bərabərdir.
- Sahə vahidi aksiomu. Tərəfi a olan kvadratın sahəsi a 2 –na bərabərdir
Həndəsənin fəza fiqurlarını öyrənən bölməsi stereometriya (yunan sozü: Stereos- fəza, metreo-ölçürəm) adlanır. Streometriyada baxılan bütün nöqtələr çoxluğuna fəza deyilir.
Stereometriyada üç anlayış: nöqtə, düz xətt və müstəvi tərifsiz qəbul olunur.Həndəsədə istənilən nöqtələr çoxluğu fiqur adlanır. Nöqtə, düz xətt, müstəvi və fəza da fiqurlardır.

Planimetriyada bilidiyimiz bütün işarələr stereometriyada da öz mənasında işlədilir. Müstəviləri, adətən, yunan əlifbasının kiçik hərfləri ilə işarə edirlər. α, β, γvə s. A, B və C nöqtələrindən keçən müstəvini isə (α, β) kimi işarə edirlər.
Əsas anlayişlarin ən mühüm xassələri streometriya aksiomlarında ifadə olunur.
AKSİOM 1 ( aidlik aksiomu)
Fəzada düz xəttlər və müstəvilər var. Hər bir düz xəttə və hər bir müstəviyə aid olan və aid olmayan nöqtələr var.

AKSİOM 2 ( Müstəvi aksiomu)
Bir düz xətt üzərində olmayan üç nöqtədən bir və yalnız bir müstəvi keçir
AKSİOM 3 ( planametriya aksiomu)
Planametriyanıın bütün alsiomları və teoremləri fəzanın hər bir müstəvisində doğrudur.

Fəzada müstəvilərin iki qarşılıqlı vəziyyəti ola bilər, ortaq nöqtəsi olan müstəvilərə kəsişən, ortaq nöqtəsi olmayan müstəvilərə kəsişməyən müstəvilər deyilir.
AKSİOM 4 ( Müstəvilərin kəsişmə aksiomu)
İki müxtəlif müstəvinin ortaq nöqtəsi varsa, onlar bu nöqtələrdən keçən düz xətt boyunca kəsişirlər
AKSİOM 5 ( Fəzanın bölünməsi aksiomu)
Fəzadakı hər bir müstəvi fəzanın bu müstəviyə aid olmayan nöqtələrini aşağıdakı şərti ödəyən iki çoxluğa ayrılır:
- Eyni çoxluğa aid olan ixtiyari iki nöqtəni birləşdirən parça bu müstəvini kəsmir.
- Müxtəlif çoxluqlara aid olan istənilən iki nöqtəni birləşdirən parça müstəvini kəsir.

α müstəvisi ilə bu çoxluqların birindən ibarət fiqura sərhəddi α müstəvisi olan yarımfəza deyilir.
Müxtəlif müstəvilərdə yerləşən qabarıq çoxbucaqların bərabərliyi və oxşarliğı da planimetriyada olduğu kimi qəbul edilir.
