Çevrə

Müstəvi üzərində yerləşən nöqtədən eyni məsafədə olan nöqtələr çoxluğuna çevrə deyilir.
AO=OB=OC=R-çevrənin radiusudur.
Çevrə mövzusu üç hissədən ibarətdir:
Ø Çevrənin elementləri
Ø Çevrədə bucaq münasibətləri
Ø Çevrədə metrik münasibətlər

Çevrənin elementləri
* Çevrə ilə bir ortaq nöqtəsi olan düz xəttə toxunan deyilir. AB toxunan, K toxunma nöqtəsidir.
* Çevrə ilə iki ortaq nöqtəsi olan düz xəttə kəsən deyilir. CD kəsəndir.



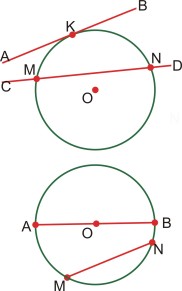
* Kəsənin çevrə ilə məhdudlanmış hissəsinə vətər deyilir.
* Çevrənin ən böyük vətərinə diametr deyilir.
* Çevrənin hər hansı bir hissəsinə qövs deyilir və “” kimi işarə edilir. Şəkildə ÁµB qövsü göstərilmişdir.

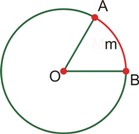
Qeyd: Qövsün dərəcə ölçüsü dərəcə və ya radianla göstərilir.

Çevrənin elementləri:

1. Çevrənin iki nöqtəsini birləşdirən düz xətt parçasına vətər deyilir.
2. Müstəvinin çevrə ilə əhatə olunmuş hissəsinə dairə deyilir.
3. Çevrənin mərkəzindən keçən vətərə diametr deyilir.
4. Çevrə ilə bir ortaq nöqtəsi olan düz xəttə toxunan deyilir.
5. Eyni mərkəzli iki müxtəlif çevrəyə konsentrik çevrələr deyilir.

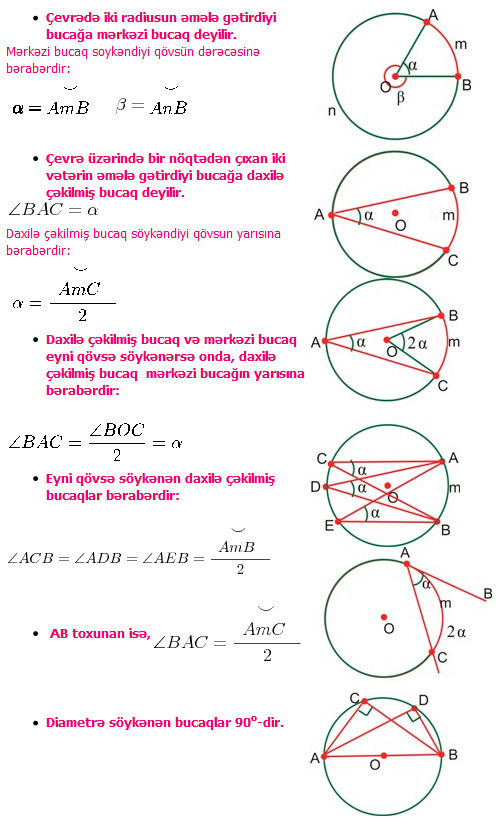
Çevrədə bucaq münasibətləri

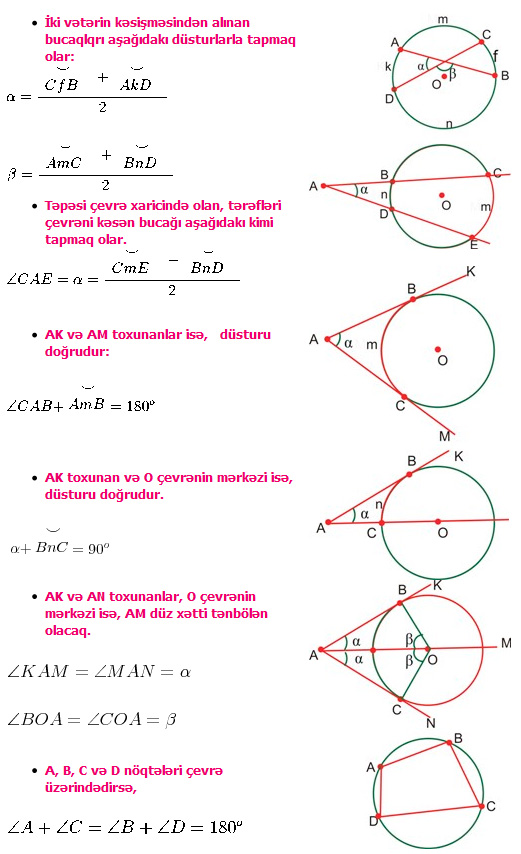
Çevrədə metrik münasibətləri

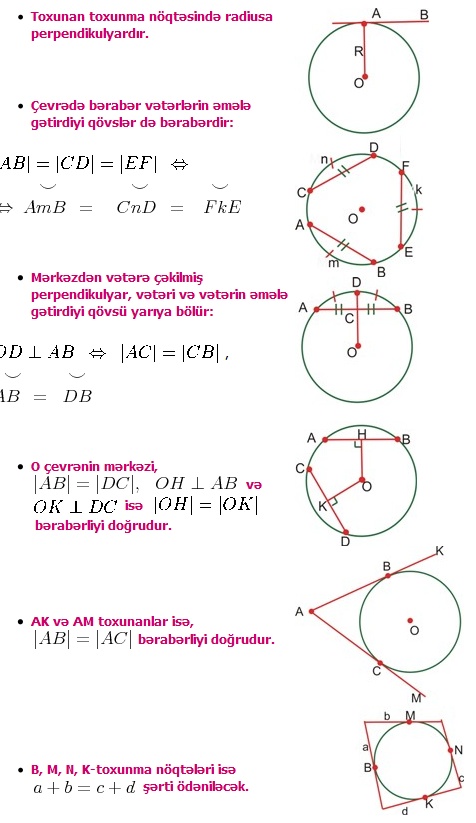
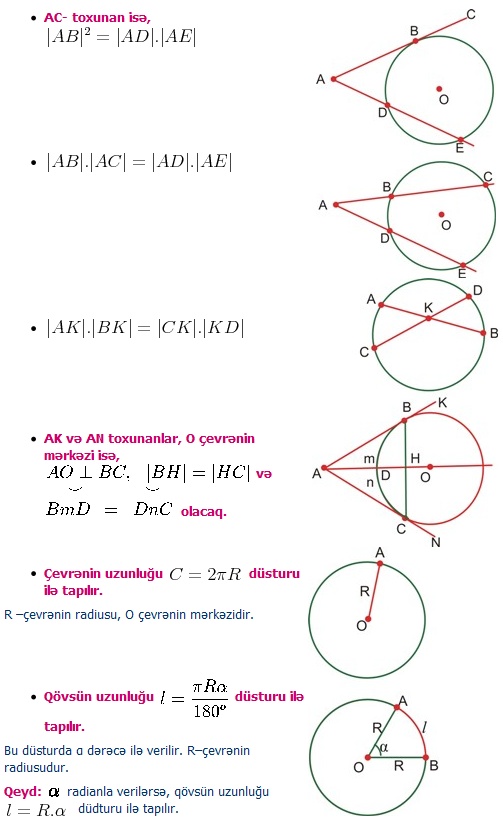
Çevrənin xassələri:

• Çevrənin uzunluğunun dimaterinə nisbəti onların qiymətindən asılı olmayaraq bütün çevrələr üçün eynidir. Bu nisbət π-dir.
• Verilmiş uzunluğa malik qapalı əyrilərdən müstəvi üzərində ən çox sahəni əhatə edən fiqur çevrədir.
• Düz xəttin çevrə ilə ya 1 (toxunan), ya 2 (kəsən) ortaq nöqtəsi ola bilər, yaxud heç bir ortaq nöqtəsi ola bilməz.
• Çevrəyə toxunan həmişə bir tərəfi kəsişmə nöqtəsində olan diametrə perpendikilyardır.
• Bir düz xətt üzərində olmayan 3 nöqtədən yalnız və yalnız bir çevrə keçirmək olar.
• İki çevrənin toxunma nöqtələri onların mərkəzlərini birləşdirən düz xətt üzərində yerləşir.

Çevrə — müstəvi üzərində verilmiş nöqtədən müsbət r məsafədə olan nöqtələr çoxluğuna deyilir.