Stereometriya aksiomları,paralelellik
Stereometriya aksiomları,paralelellik
STEREOMETRİYA AKSİOMLARINDAN ALINAN NƏTİCƏLƏR
Stereometriya aksiomlarından bir necə mühüm nəticələr alınır. Bu nəticələr aşağıdakı teoremlərlə ifadə olunur.
Teorem 1: Düz xəttin müstəviyə aidliyi
Düz xətlə müstəvinin iki ortaq nöqtəsi varsa, bu düz xətt müstəvi üzərindədir.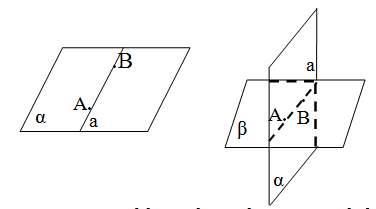
İsbatı: Tutaq ki, a düz xəttinin A və B nöqtələri α müstəvisi üzərindədir. a düz xəttinə və α müstəvisinə aid olmayan M nöqtəsi götürək.
A, B və M nöqtələrindən β müstəvisi keçirək (aksiom 2). α və β müstəvilərinin kəsişmə xətti A və B nöqtələrindən keçdiyinə görə a düz xətti ilə üst-üstə düşür.
Kəsişmə xəttinin hər bir nöqtəsi α müstəvisinin nöqtəsi olduğundan a düz xəttinin də hər bir nöqtəsi α müstəvisinin nöqtəsidir. Yəni a düz xətti α müstəvisi üzərindədir. Teorem isbat olundu.
Teorem 2:
Düz xətt və ona aid olmayan nöqtədən bir və yalnız müstəvi keçir
İsbatı: Verilən düz xətt a, ona aid olmayan nöqtə isə A olsun. a düz xətti üzərində B və C nöqtələri götürək. A, B və C nöqtələri bir düz xətt üzərində olmayan üç nöqtə olduğundan bir və yalnız müstəvi keçir (aksiom 2).
 Bu müstəvini α adlandıraq. Teorem 1-ə əsasən a düz xətti α müstəvisi üzərindədir. A nöqtəsi də α müstəvisi üzərində olduğundan bu, tələb olunan müstəvidir. Göstərək ki, bu müstəvi yeganədir. Doğrudan da a düz xəttindən və A nöqtəsindən keçən istənilən müstəvi bir düz xətt üzərində olmayan A, B və C nöqtələrindən keçdiyi üçün α müstəvisi ilə eynidir (aksiom 2). Teorem isbat olundu.
Bu müstəvini α adlandıraq. Teorem 1-ə əsasən a düz xətti α müstəvisi üzərindədir. A nöqtəsi də α müstəvisi üzərində olduğundan bu, tələb olunan müstəvidir. Göstərək ki, bu müstəvi yeganədir. Doğrudan da a düz xəttindən və A nöqtəsindən keçən istənilən müstəvi bir düz xətt üzərində olmayan A, B və C nöqtələrindən keçdiyi üçün α müstəvisi ilə eynidir (aksiom 2). Teorem isbat olundu.
Teorem 3:
Iki kəsişən düz xətdən bir və yalnız bir müstəvi keçir

FƏZADA XƏTLƏRİN PARALELLİYİ
Fəzada bir ortaq nöqtəsi olan iki düz xətlə kəsişən düz xəttlər deyilir.
Bir müstəvi üzərində olan və kəsişməyən düz xətlərə paralel düz xətlər deyilir.
Teorem 1:
Fəzada düz xətt xaricində götürülmüş nöqtədən həmin düz xəttə paralel bir və yalnız bir düz xətt keçir

Teorem 2:
Eyni bir düz xəttə paralel olan iki düz xətt paraleldir
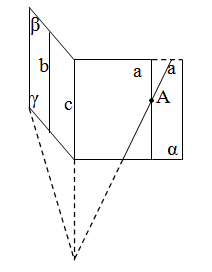
Teorem 3:
Müstəvi üzərinda olmayan düz xətt, müstəvi üzərindəki hər hansı bir düz xəttə paraleldirsə, onda bu müstəvinin özünə də paraleldir

Teorem 4:
Bir müstəvi β ikinci müstaviyə (α) paralel olan düz xətdən (a) keçib və onu kəsərsə, alınan kəsişmə xətti (a1) verilən düz xəttə (a) paralel olar.
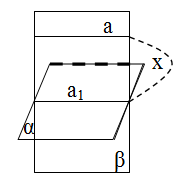
Çarpaz düz xətlər.
Bir müstəvi üzərində olmayan düz xətlərə çarpaz düz xətlər deyilir.
Teorem 5: düz xətlərin çarpazlıq əlaməti
İki düz xətdən biri ikincisindən keçən hər hansı müstəvini ikinci düz xəttə aid olmayan nöqtədə kəsərsə, onda bu düz xətlər çarpazdır
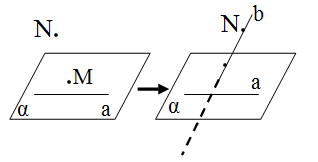
Paralel Müstəvilər
Bilirik ki, iki müstəvinin bir ortaq nöqtəsi varsa, onlar bu nöqtədən keçən düz xətt boyunca kəsişir. Belə müstəvilərə kəsişən müstəvilər deyilir.

İki müstəvinin bir düz xətt üzərində olmayan üç ortaq nöqtəsi olarsa, onlar üst-üstə düşür, yəni eyni müstəvi olur.

Ortaq nöqtəsi olmayan müstavilərə paralel müstəvilər deyilir. α//α1
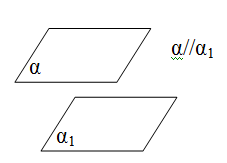
Teorem 10 Müstəvilərin paralellik əlaməti
Bir müstəvinin iki kəsişən düz xətti, uyğun olaraq, o biri müstəvinin iki kəsişən düz xəttinə paraleldirsə, bu müstəvilər paraleldir.
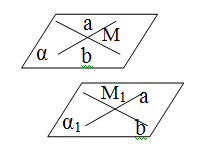
Nəticə: Iki çarpaz düz xətdən bir-birinə paralel, yalnız iki müstəvi keçir.
Teorem 11
Iki paralel müstəvini üçüncü müstəvi kəsirsə, alınan kəsişmə xətləri paraleldir.
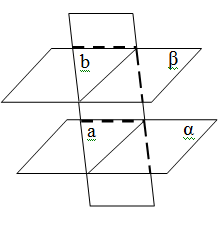
Teorem 12
Paralel düz xətlərin paralel müstəvilər arasında qalan parçaları bərabərdir.
Stereometriya aksiomlarından bir necə mühüm nəticələr alınır. Bu nəticələr aşağıdakı teoremlərlə ifadə olunur.
Teorem 1: Düz xəttin müstəviyə aidliyi
Düz xətlə müstəvinin iki ortaq nöqtəsi varsa, bu düz xətt müstəvi üzərindədir.

İsbatı: Tutaq ki, a düz xəttinin A və B nöqtələri α müstəvisi üzərindədir. a düz xəttinə və α müstəvisinə aid olmayan M nöqtəsi götürək.
A, B və M nöqtələrindən β müstəvisi keçirək (aksiom 2). α və β müstəvilərinin kəsişmə xətti A və B nöqtələrindən keçdiyinə görə a düz xətti ilə üst-üstə düşür.
Kəsişmə xəttinin hər bir nöqtəsi α müstəvisinin nöqtəsi olduğundan a düz xəttinin də hər bir nöqtəsi α müstəvisinin nöqtəsidir. Yəni a düz xətti α müstəvisi üzərindədir. Teorem isbat olundu.
Teorem 2:
Düz xətt və ona aid olmayan nöqtədən bir və yalnız müstəvi keçir
İsbatı: Verilən düz xətt a, ona aid olmayan nöqtə isə A olsun. a düz xətti üzərində B və C nöqtələri götürək. A, B və C nöqtələri bir düz xətt üzərində olmayan üç nöqtə olduğundan bir və yalnız müstəvi keçir (aksiom 2).
 Bu müstəvini α adlandıraq. Teorem 1-ə əsasən a düz xətti α müstəvisi üzərindədir. A nöqtəsi də α müstəvisi üzərində olduğundan bu, tələb olunan müstəvidir. Göstərək ki, bu müstəvi yeganədir. Doğrudan da a düz xəttindən və A nöqtəsindən keçən istənilən müstəvi bir düz xətt üzərində olmayan A, B və C nöqtələrindən keçdiyi üçün α müstəvisi ilə eynidir (aksiom 2). Teorem isbat olundu.
Bu müstəvini α adlandıraq. Teorem 1-ə əsasən a düz xətti α müstəvisi üzərindədir. A nöqtəsi də α müstəvisi üzərində olduğundan bu, tələb olunan müstəvidir. Göstərək ki, bu müstəvi yeganədir. Doğrudan da a düz xəttindən və A nöqtəsindən keçən istənilən müstəvi bir düz xətt üzərində olmayan A, B və C nöqtələrindən keçdiyi üçün α müstəvisi ilə eynidir (aksiom 2). Teorem isbat olundu.Teorem 3:
Iki kəsişən düz xətdən bir və yalnız bir müstəvi keçir

FƏZADA XƏTLƏRİN PARALELLİYİ
Fəzada bir ortaq nöqtəsi olan iki düz xətlə kəsişən düz xəttlər deyilir.
Bir müstəvi üzərində olan və kəsişməyən düz xətlərə paralel düz xətlər deyilir.
Teorem 1:
Fəzada düz xətt xaricində götürülmüş nöqtədən həmin düz xəttə paralel bir və yalnız bir düz xətt keçir

Teorem 2:
Eyni bir düz xəttə paralel olan iki düz xətt paraleldir

Teorem 3:
Müstəvi üzərinda olmayan düz xətt, müstəvi üzərindəki hər hansı bir düz xəttə paraleldirsə, onda bu müstəvinin özünə də paraleldir

Teorem 4:
Bir müstəvi β ikinci müstaviyə (α) paralel olan düz xətdən (a) keçib və onu kəsərsə, alınan kəsişmə xətti (a1) verilən düz xəttə (a) paralel olar.

Çarpaz düz xətlər.
Bir müstəvi üzərində olmayan düz xətlərə çarpaz düz xətlər deyilir.
Teorem 5: düz xətlərin çarpazlıq əlaməti
İki düz xətdən biri ikincisindən keçən hər hansı müstəvini ikinci düz xəttə aid olmayan nöqtədə kəsərsə, onda bu düz xətlər çarpazdır

Paralel Müstəvilər
Bilirik ki, iki müstəvinin bir ortaq nöqtəsi varsa, onlar bu nöqtədən keçən düz xətt boyunca kəsişir. Belə müstəvilərə kəsişən müstəvilər deyilir.

İki müstəvinin bir düz xətt üzərində olmayan üç ortaq nöqtəsi olarsa, onlar üst-üstə düşür, yəni eyni müstəvi olur.

Ortaq nöqtəsi olmayan müstavilərə paralel müstəvilər deyilir. α//α1

Teorem 10 Müstəvilərin paralellik əlaməti
Bir müstəvinin iki kəsişən düz xətti, uyğun olaraq, o biri müstəvinin iki kəsişən düz xəttinə paraleldirsə, bu müstəvilər paraleldir.

Nəticə: Iki çarpaz düz xətdən bir-birinə paralel, yalnız iki müstəvi keçir.
Teorem 11
Iki paralel müstəvini üçüncü müstəvi kəsirsə, alınan kəsişmə xətləri paraleldir.

Teorem 12
Paralel düz xətlərin paralel müstəvilər arasında qalan parçaları bərabərdir.
