Riyaziyyat kateqoriyası üzrə məqalələr
Ramanucan
 19-cu əsrin sonunda Hindistanın cənubunda kasıb bir ailədə Srinivasa Ramanucan Ayenqor adlı bir oğlan dünyaya gəlir. Onun ailəsi zənginliyi ilə fərqlənməsə də, brahmanlar kastasına daxil idi və ənənə və dini ayinləri müqəddəs hesab edirdilər. Buna görə də gənc Ramanucanın bütün təhsil və tərbiyəsi yalnız bir şeyə gətirib çıxarırdı: O atasının yolunu davam etdirməli və məmur olmalı idi.
19-cu əsrin sonunda Hindistanın cənubunda kasıb bir ailədə Srinivasa Ramanucan Ayenqor adlı bir oğlan dünyaya gəlir. Onun ailəsi zənginliyi ilə fərqlənməsə də, brahmanlar kastasına daxil idi və ənənə və dini ayinləri müqəddəs hesab edirdilər. Buna görə də gənc Ramanucanın bütün təhsil və tərbiyəsi yalnız bir şeyə gətirib çıxarırdı: O atasının yolunu davam etdirməli və məmur olmalı idi.Lakin Ramanucanı lap kiçik yaşlarından tamamilə başqa bir şey maraqlandırırdı. O çox da təhsilli olmayan Hindistanda heç də asan məsələ olmayan rəqəm və tənliklərin həllinə maraq göstərir. Uşaq dəhşətıi dərəcədə məlumat azlığından əziyyət çəkirdi. Onun demək olar ki, riyaziyyata aid heç bir kitabı yox idi və kitab əldə etmək üçün hətta oğurluq belə etməyə hazır idi. Ramanucan hələ hənc yaşında olarkən belə bir çox teorem və düstürları kəşf etmişdir.
ZM teoremi
İsbatı:ABCD ixtiyari qabarıq dördbucaqlısı verilmişdir. İsbat edək ki,
A1B1C1D1 paraleloqramdır. ABCD dördbucaqlısının diaqonallarını çəkək. CB diaqonalı ABC və CBD üçbucaqlarını əmələ gətirmişdir. A1B1 ABC üçbucağının orta xəttidir. Üçbucağın orta xəttinin xassəsinə görə, A1B1 AB-nin yarısına bərabərdir. Orta xətti x-la işarə etsək, CB-də 2x olur. CBD üçbucağında isə, CB 2x-sa, C1D1 orta xətt olduğu üçün x-a bərabərdir. AD diaqonalı isə, ADC və ABD üçbucaqlarını əmələ gətirmişdir. A1C1 parçası ADC üçbucağının orta xəttidir. Orta xəttin xassəsinə görə A1C1 AD-nin yarısına bərabərdir.A1C1-i y-lə işarə etsək etsək, AD 2y olar.B1D1 isə ABD üçbucağının orta xəttidir. AD 2y-sə, B1D1 orta xətt olduğu üçün y-ə bərabərdir. Paraleloqramın əlamətinə görə, qarşı tərəfləri cüt-cüt bərabər olan dördbucaqlı paraleloqram adlanır.
Teorem isbat edildi.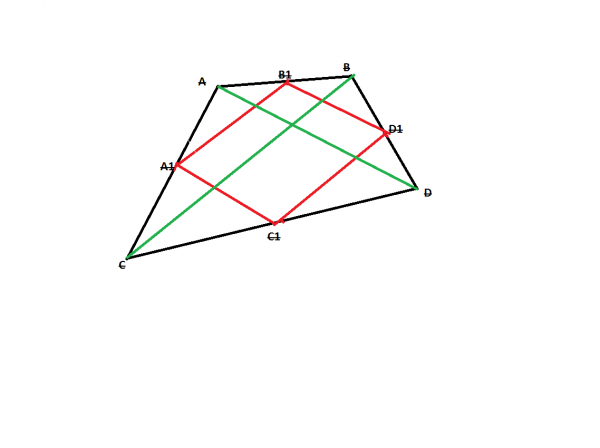
Sadə hökmlər və onların növləri
Hökmlər sadə və mürəkkəb olmaqla iki növə bölünür. İki anlayış arasında əlaqəni ifadə edən hökmə sadə hökm deyilir.Məsələn, “Məntiq elmdir”, “Cəfər sürücüdür”.Mürəkkəb hökmlər isə bir neçə sadə hökmü birləşdirir. Sadə hökmlərin özü də aşağıdakı üç yerə bölünür.
1) Atributiv ( xassə, əlamət sözündəndir ) hökmlər.Atributiv hökm predmetin əlaməti haqqında fikirdir.Burada müəyyən xassənin, əlamətin və halın predmetə məxsus olması iqrar və ya inkar edilir.Məsələn, “Bakı şəhəri “qara qızıl” diyarıdır”, “İnsan şüurludur” və s.Atributiv hökmlərin formulu belədir: “S – P-dir” S – P deyil”.
S hökmün subyektini, yəni hökmün predmeti haqqındakı məfhumu, P isə hökmün predikatını, yəni hökmün predmetinin əlaməti haqqındakı məfhumu ifadə edir.
Riyaziyyatın tarixi sirləri
 Riyaziyyat “matesis” (μάθημα) – yunan dilində “mən bilirəm” və ya “elm” mənasını verir. “Riyaziyyat” sözünə ilk dəfə b.e.ə. 550-ci ildə Pifaqor məktəbində rast gəlinmişdir. Pifaqor həm də riyaziyyat tarixində ən çox tənlik yaradan alimdir.
Riyaziyyat “matesis” (μάθημα) – yunan dilində “mən bilirəm” və ya “elm” mənasını verir. “Riyaziyyat” sözünə ilk dəfə b.e.ə. 550-ci ildə Pifaqor məktəbində rast gəlinmişdir. Pifaqor həm də riyaziyyat tarixində ən çox tənlik yaradan alimdir.
Riyaziyyat insanlıq tarixinin ən qədim elmlərindəndir. Bütün elmlərin açarı hesab edilir, onun köməyilə kainatı anlamaq olar. Sayın hesablaması əldə on barmağın olmasını mənimsədikdən sonra yaranmışdır. Qədim insan üçün barmaqlar ən yaxşı hesab vasitəsi idi. Mayya və çukçalara (Kamçatkada yaşayan xalq) görə 20-lik say sistemi mövcud idi. Onlar ayaq barmaqları ilə də hesablama aparırdılar.
İlk riyaziyyatçı qadın yunanlı Hipatiya olmuşdur. O, IV-V əsrlərdə yaşamışdır.
Hesab
Sayarkən istifadə etdiyimiz ədədlərə natural ədədlər deyilir. Natural ədədlər üzərində toplama, çıxma, vurma, bölmə, qüvvətə yüksəltmə və kökalma əməllərini yerinə yetirmək olar. Natural ədədlər çoxluğu «N» kimi işarə olunur.
Natural ədədlər, onların əksi və 0 birlikdə tam ədədlər çoxluğunu əmələ gətirir. Tam ədədlər çoxluğu «Z» kimi işarə olunur.
Rasional ədədlər — m/n şəklində göstərilə bilən ədədlərə deyilir, burada m tam ədəd, n isə natural ədəddir. Rasional ədədlər çoxluğu «Q» ilə işarə olunur.
Stereometriya aksiomları
Stereometriya aksiomlarından bir necə mühüm nəticələr alınır. Bu nəticələr aşağıdakı teoremlərlə ifadə olunur.
Teorem 1: Düz xəttin müstəviyə aidliyi
Düz xətlə müstəvinin iki ortaq nöqtəsi varsa, bu düz xətt müstəvi üzərindədir.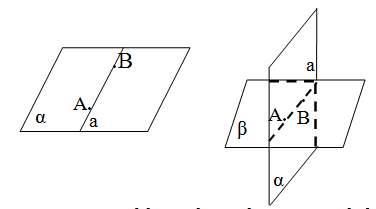
İsbatı: Tutaq ki, a düz xəttinin A və B nöqtələri α müstəvisi üzərindədir. a düz xəttinə və α müstəvisinə aid olmayan M nöqtəsi götürək.
A, B və M nöqtələrindən β müstəvisi keçirək (aksiom 2). α və β müstəvilərinin kəsişmə xətti A və B nöqtələrindən keçdiyinə görə a düz xətti ilə üst-üstə düşür.
Kəsişmə xəttinin hər bir nöqtəsi α müstəvisinin nöqtəsi olduğundan a düz xəttinin də hər bir nöqtəsi α müstəvisinin nöqtəsidir. Yəni a düz xətti α müstəvisi üzərindədir. Teorem isbat olundu.
Ardıсıllıqlar
1. Ardıсıllıqlar
Müəyyən riyazi qanunla düzülmüş ədədlərin yaratdığı ardıсıllığa ədədi ardıсıllıq deyilir. Sonu olan ardıсıllıqlar yığılan ardıсıllıq adlanır.
2. Ədədi ardıсılıq, ədədi silsilə və düsturları.
Həmin ardıсıllıqda, özündən ikinсidən başlayaraq hər bir həddi özündən əvvəlki hədlə eyni bir ədədin сəminə bərabər olan ədədi ardıcıllığa ədədi silsilə deyilir.
Düzgün çoxüzlülər
Yaxşı tanıdığımız kub düzgün çoxüzlüdür. Çünki onun bütün üzləri kvadratdır, hər bir təpəsindən üç til çıxır.
Teorem 29.
Düzgün çoxüzlünün hər bir üzünün tərəfləri sayı 5 dən çox ola bilməz.
Əgər düzgün çoxüzlünün üzləri bərabərtərəfli üçbucaq olsa, onda onun hər bir təpəsindəki müstəvi bucaqlarının sayı 3.4 və ya 5 ola bilər.Bu zaman düzgün tetradr (dördüzlü), düzgün oktaedr (şəkkizüzlü) və düzgün ikosaedr (iyirmiüzlü) alınır.
Çoxüzlü anlayışı,prizma,paraleliped
Cisim və səth
Stereometriyanın əsəs predmeti həndəsi cisimlər və onların səthidir. Həndəsi cisim və yaxud sadə cisim anlayışı həyatdan, praktikadan, təbiətdən götürülmüşdür. Həndəsi cisim-real mövcud olan fiziki cismin fəzada tutduğu hissədir. Fiziki cismin fiziki və digər xassələri həndəsi cisimdə nəzərə alınmır. Həndəsi cisim üçün mühüm keyfiyyət real fiziki cismin forması və tutduğu fəza hissəsidir.
Cismə aid olmayan nöqtədən cismin səthinin ən yaxın nöqtəsinə qədər məsafəyə nöqtədən cismə qədər məsafə deyilir.
