Riyaziyyat kateqoriyası üzrə məqalələr

Bir çoxüzlü bucaq götürək və onun bütün tillərini kəsən müstəvi keçirək. Çoxüzlü bucaqın S təpəsinin aid olduğu yarımfəzada SABDEF çoxüzlüsü alınır. Bu çoxüzlünün bir üzü ABCDEF çoxbucaqlısı qalan üzləri isə bir təpəsi S olan ortaq təpəsi üçbucaqlıdır. ASB, BSC,........, FSA, belə çoxüzlülər piramida adlanır.

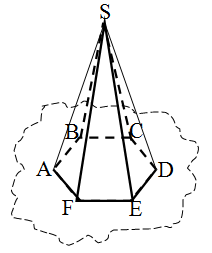Ortaq təpəli üçbucaqlara piramidanın yan üzləri, onların birləşməsinə piramidanın yan səthi, çoxbucaqlıya piramidanın oturacağı, bütün yan üzlərin ortaq tərəfinə piramidanın yan tilləri, təpədən oturacaq müstəvisinə çəkilmiş perpendikulyara piramidanın hündürlüyü deyilir.

Perpendikulyar və mail
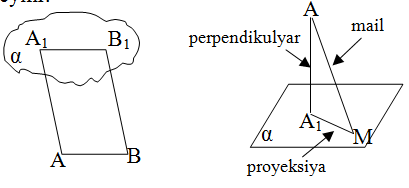
Paralel proyeksiyada istiqamət proyeksiya müstəvisinə paralel olmayan düz xətdir. Bu düz xətt xüsusi halda həmin müstəviyə perpendikulyar ola bilər.
İstiqaməti proyeksiya müstəvisinə perpendikulyar olan paralel proyeksiyaya ortoqonal proyeksiya deyilir.
A nöqtəsindən α müstəvisinə perpendikulyar düz xətt çəkək. Bu düz xəttin α müstəvisi ilə kəsişmə nöqtəsi A1 olsun AA1 parçasına A nöqtəsindən α müstəvisinə çəkilmiş perpendikulyar deyilir. A1 nöqtəsinə perpendikulyarın müstəvi üzərindəki oturacağı deyilir. A1 nöqtəsinə perpendikulyarın müstəvi üzərindəki oturacağı deyilir.

Həndəsə kursunun məntiqi qurulmasında aksiomların müstəsna əhəmiyyatini nəzərə alaraq planimetreyanın aksiomlarını yadımıza salaq:

1. Aidolma aksiomu. Düz xəttin üzərində olan nöqtələr və onun üzərində olmayan nöqtələr var.
2. Düz xətt aksiomu. İki nöqtədən bir yalnız bir düz xətt keçir.
3. Nöqtələrin düz xətt üzərində yerləşməsi aksionu. Düz xəttin ixtiyari 3 nöqtəsindən biri yalniz biri qalan ikisi arasında yerləşir.
4. Düz xəttin bölünməsi aksionu. Düz xəttin ixtiyari A nöqtəsi bu düz xəttin qalan nöqtələrini aşağıdakı şərtləri ödəyən iki çoxluğa ayırır: eyni çoxluğa aid iki nöqtə A nöqtəsinin bir tərəfində yerləşir, müxtəlif çoxluqlara aid iki nöqtə A nöqtəsinin müxtəlif tərəfində yerləşir.

Həndəsə — həndəsi fiqurların xassələri  haqqında  elmdir.
GEOMETRIYA yunan sözüdür. Azərbaycan dilində tərcümasi, YERÖLÇMƏ deməkdir.
Həndəsi fiqurlara aid nümunələr: 

Riyaziyyatın Ən əsas həll olunmamış problemləri «Minilliyin Problemləri» — «Millenium Problems» adlanır. Bu ad altında 7 problem vardır ki, onlardan biri — Poinkare fərziyyəsi rusiyalı riyaziyyatçı Qriqori Yakovleviç Perelman tərəfindən 2010-cu ilin sentyabrında sübuta yetirilmişdir. Bu ad altında problemlərin həllinə Amerikanın Kley İnstitutu (Clay İnstitute) tərəfindən 1000000 USD civarında mükafat qoyulmuşdur. Lakin indi o məsələlərə girişməyəcəyik.
Əlavə Ədədlər Nəzəriyyəsi üzərindən bəzi problemləri nəzərinizə çatdırmaq istəyirəm.
1. Qoldbax hipotezi (Goldbach hypothesis):
«2-dən böyük cüt ədədlər 2 sadə ədədin cəmi şəklində göstərilə bilər.»
Maraqlısı burasındadır ki, bu fərziyyənin nə doğruluğu, nə də əksi isbat oluna bilib.
Alman riyaziyyatçısı Kristian Qoldbax məşhur riyaziyyatçı Leonard Eylerə (Leonhard Euler) 1742-ci il tarixli məktubunda bu fərziyyəni qeyd etmişdi.

2. Kollatz fərziyəsi (Collatz conjecture):
Fərziyyə belə ifadə olunur:
«Hər hansı bir müsbət tam (natural) ədəd:
1. Cütdürsə, 2-ə bölündükdə;
2. Təkdirsə, 3-ə vurulub üzərinə 1 əlavə etdikdə;
3. Və alınan təzə ədəd üzərində də bu əməliyyatları periodik şəkildə yerinə yetirsək, son ədəd mütləq 1 olacaqdır.»
Bu fərziyyənin əksi demək olar ki, mümkün deyil. Amma isbat edən də olmayıb. Bu fərziyyəni artıq nəzəriyyə kimi istifadə edərək, müəyyən ədəddən 1 ədədinin alınmasınadək proseslərin sayının hesablamasının tətbiqində araşdırmalar aparılır.
Alman riyaziyyatçısı olan Lotar Kollatz (Lothar Collatz) 1937-ci ildə, 27 yaşında ikən bu fərziyyəni irəli sürmüşdür və hələ də isbat edən olmamışdır.


Ardı var...

Müstəvi üzərində yerləşən nöqtədən eyni məsafədə olan nöqtələr çoxluğuna çevrə deyilir.
AO=OB=OC=R-çevrənin radiusudur.
Çevrə mövzusu üç hissədən ibarətdir:
Ø Çevrənin elementləri
Ø Çevrədə bucaq münasibətləri
Ø Çevrədə metrik münasibətlər

Bucağın aşağıdakı növləri vardır:
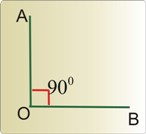
Ø Düz bucaq
Dərəcə ölçüsü 90°-yə bərabər olan bucağa düz bucaq deyilir.

Ø Açıq bucaq
Dərəcə ölçüsü 180°-yə bərabər olan bucaga açıq bucaq deyilir.

1. Həndəsənin əsas anlayişları asağıdakılardır:
Ø Nöqtə
Ø Düz xətt
Ø Yarım düz xətt və ya şüa
Ø Parça
Ø Bucaq

Əvvəla mən Fibonaççi ədədləri haqqında məlumat vermək istərdim və bununçün də Vikipediaya müraciət edirəm:
«Riyaziyyatda, Fibonaççi ədədləri aşağıdakı kimi təyin olunur:
Tərifə əsasən, ilk iki Fibonaççi ədədləri 0 və 1-dir. Sonra gələn ədəd özündən əvvəlki ilk iki qonşusunun cəminə bərabərdir. Bəzi mənbələrdə sıranın ilk ədədi 0 yox, 1 götürülür.
Riyazi dildə, Fibanoççi sırası Fn aşağıdakı rekkurent düsturla verilir harda ki, F0 = 0 və F1 = 1.
Fibonaççi sırası Pizali Leonardonun adı ilə bağlıdır.